
Use the information below to generate a citation. Then you must include on every digital page view the following attribution: If you are redistributing all or part of this book in a digital format, Step 3: Click on the 'Reset' button to clear the fields and find the sum of. Step 2: Click on the 'Calculate' button to find the sum of the arithmetic sequence. There are two ways to find the sum of a finite arithmetic sequence. The sum of an infinite arithmetic sequence is either, if d > 0, or -, if d < 0. The sum of the first 4 terms of the arithmetic sequence is 12.

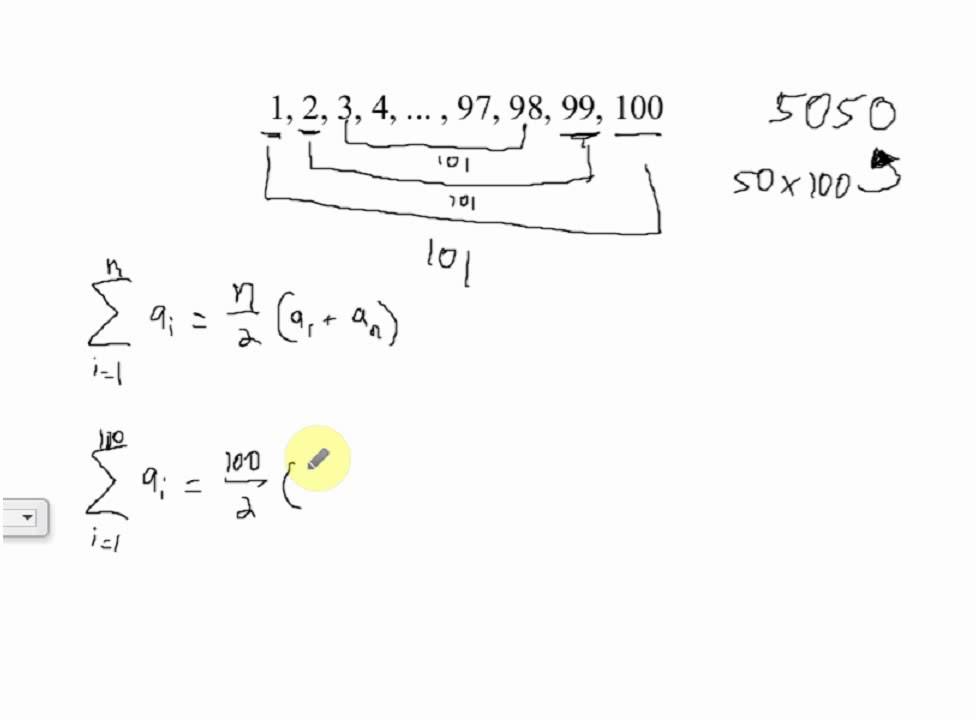
The second term of an arithmetic sequence is 7. Find the sum of the positive terms of the arithmetic sequence ô ñ, ô, ó í, 9. Find the sum of the first 100 odd numbers 8. Then you must include on every physical page the following attribution: Please follow the steps below to find the sum of the arithmetic sequence: Step 1: Enter the first term (a), the common difference (d), and the number of terms (n) in the given input box. An arithmetic sequence can also be defined recursively by the formulas a 1 c, a n+1 a n + d, in which d is again the common difference between consecutive terms, and c is a constant. thAn arithmetic sequence has a 10 term of 17 and a 14th term of 30. If you are redistributing all or part of this book in a print format, Want to cite, share, or modify this book? This book uses the You can choose any term of the sequence, and add 3 to find the subsequent term. In this case, the constant difference is 3. The sequence below is another example of an arithmetic sequence. For this sequence, the common difference is –3,400. Each term increases or decreases by the same constant value called the common difference of the sequence. The values of the truck in the example are said to form an arithmetic sequence because they change by a constant amount each year. In this section, we will consider specific kinds of sequences that will allow us to calculate depreciation, such as the truck’s value. The truck will be worth $21,600 after the first year $18,200 after two years $14,800 after three years $11,400 after four years and $8,000 at the end of five years. The loss in value of the truck will therefore be $17,000, which is $3,400 per year for five years. After five years, she estimates that she will be able to sell the truck for $8,000. One method of calculating depreciation is straight-line depreciation, in which the value of the asset decreases by the same amount each year.Īs an example, consider a woman who starts a small contracting business. This decrease in value is called depreciation. The book-value of these supplies decreases each year for tax purposes. Use an explicit formula for an arithmetic sequence.Ĭompanies often make large purchases, such as computers and vehicles, for business use.Use a recursive formula for an arithmetic sequence.Find the common difference for an arithmetic sequence.


 0 kommentar(er)
0 kommentar(er)
